www.sansonettiivano.it

FUNZIONI GONIOMETRICHE
Le funzioni trigonometriche o funzioni goniometriche o funzioni circolari sono funzioni di un angolo; esse sono importanti nello studio dei triangoli e nella modellizzazione dei fenomeni periodici. Sono spesso definite come rapporti fra i lati di un triangolo rettangolo e, equivalentemente, possono essere definite come le lunghezze di diversi segmenti costruiti a partire dalla circonferenza goniometrica (circonferenza di centro (0;0) e raggio 1). Lo studio delle funzioni trigonometriche risale ai tempi dei babilonesi, e una quantità considerevole del lavoro fondamentale fu svolto dai matematici greci, indiani e persiani.
		Radianti Gradi Cos(x) Sen(x) Tang(x) Cotang(x) Sec(x) Cosec(x)
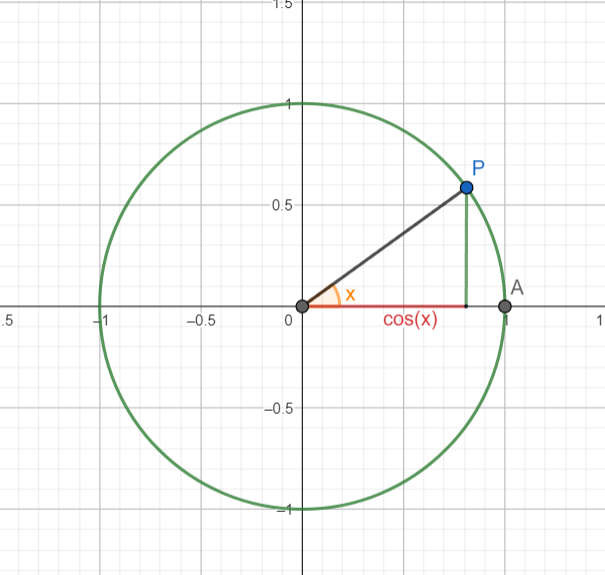
Funzione coseno Dato un triangolo rettangolo, il coseno di uno dei due angoli acuti adiacenti all'ipotenusa è definito come il rapporto tra la lunghezza del cateto adiacente all'angolo e la lunghezza dell'ipotenusa. Data la circonferenza goniometrica, il coseno di un angolo è l'ascissa del punto P individuato dall'angolo sulla circonferenza. Dopo un giro completo della circonferenza, il coseno assume sempre gli stessi valori, per questo diremo che è periodico di periodo 2π (360°) La funzione coseno è pari, quindi simmetrica rispetto all'asse delle ordinate
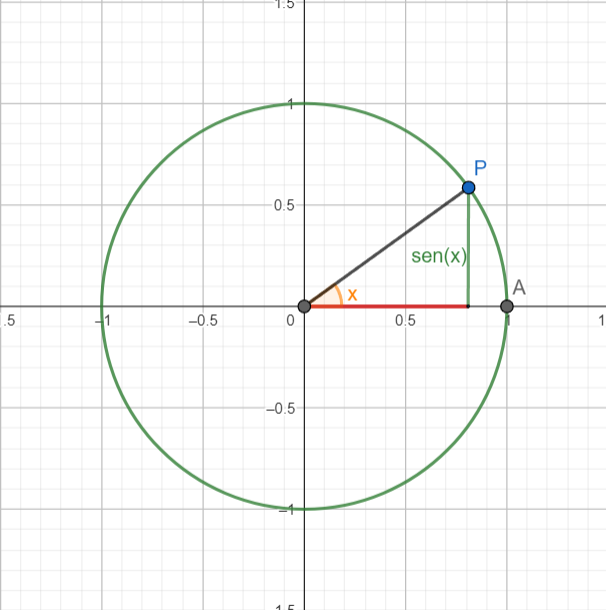
Funzione Seno Dato un triangolo rettangolo, il seno di uno dei due angoli acuti adiacenti all'ipotenusa è definito come il rapporto tra la lunghezza del cateto opposto all'angolo e la lunghezza dell'ipotenusa. Data la circonferenza goniometrica, il seno di un angolo è l'ordinata del punto P individuato dall'angolo sulla circonferenza. Dopo un giro completo della circonferenza, il seno assume sempre gli stessi valori, per questo diremo che è periodico di periodo 2π (360°) La funzione seno è dipari, quindi simmetrica rispetto all'origine del piano cartesiano.
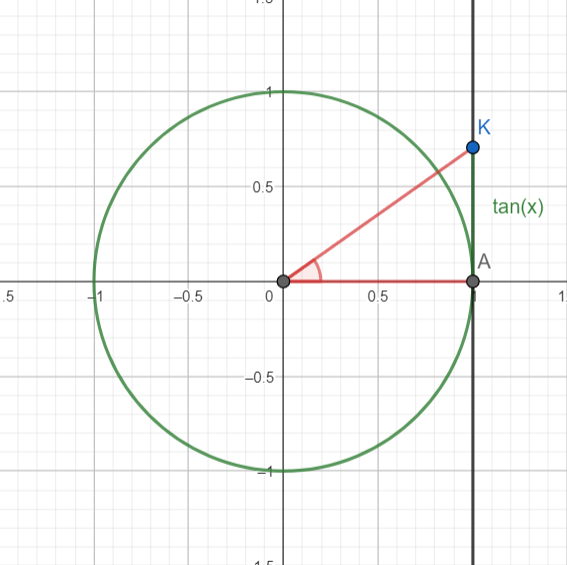
Funzione Tangente Dato un triangolo rettangolo, la tangente di uno dei due angoli acuti adiacenti all'ipotenusa è definito come il rapporto tra la lunghezza del cateto adiacente all'angolo e la lunghezza del cateto opposto all'angolo. Data la circonferenza goniometrica, la tangente di un angolo è l'ordinata del punto K individuato dall'angolo sulla tangente alla circonferenza nel punto A(1;0). Dopo mezzo giro della circonferenza, la tangente assume sempre gli stessi valori, per questo diremo che è periodica di periodo π (180°) La funzione tangente è dipari, quindi simmetrica rispetto all'origine degli assi cartesiani.
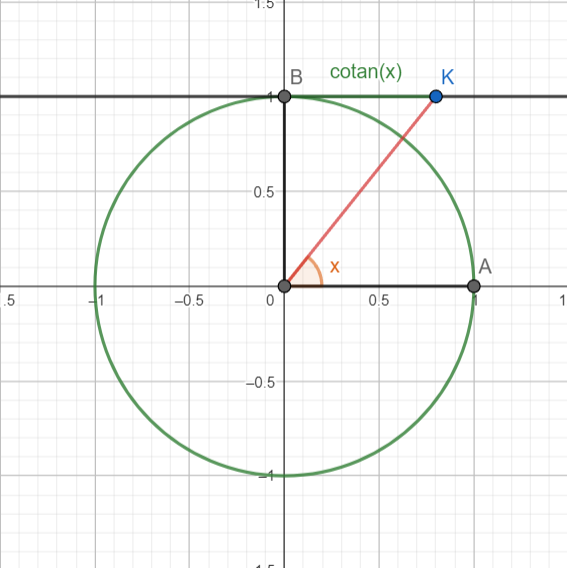
Funzione Cotangente Dato un triangolo rettangolo, la cotangente di uno dei due angoli acuti adiacenti all'ipotenusa è definito come il rapporto tra la lunghezza del cateto opposto all'angolo e la lunghezza del cateto adiacente all'angolo. Data la circonferenza goniometrica, la cotangente di un angolo è l'ascissa del punto K individuato dall'angolo sulla tangente alla circonferenza nel punto B(0;1). Dopo mezzo giro della circonferenza, la cotangente assume sempre gli stessi valori, per questo diremo che è periodica di periodo π (180°) La funzione cotangente è dipari, quindi simmetrica rispetto all'origine degli assi cartesiani.
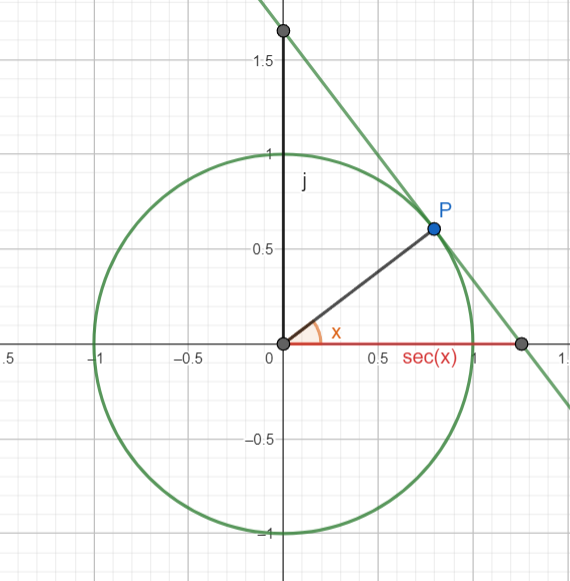
Funzione Secante Dato un triangolo rettangolo, la secante di uno dei due angoli acuti adiacenti all'ipotenusa è definito come il rapporto tra la lunghezza dell'ipotenusa e la lunghezza del cateto adiacente all'angolo. Data la circonferenza goniometrica, la secante di un angolo è il reciproco del coseno dell'angolo considerato. Dopo un giro completo della circonferenza, la secante assume sempre gli stessi valori, per questo diremo che è periodica di periodo 2π (180°) La funzione secante è pari, quindi simmetrica rispetto all'asse delle ordinate.
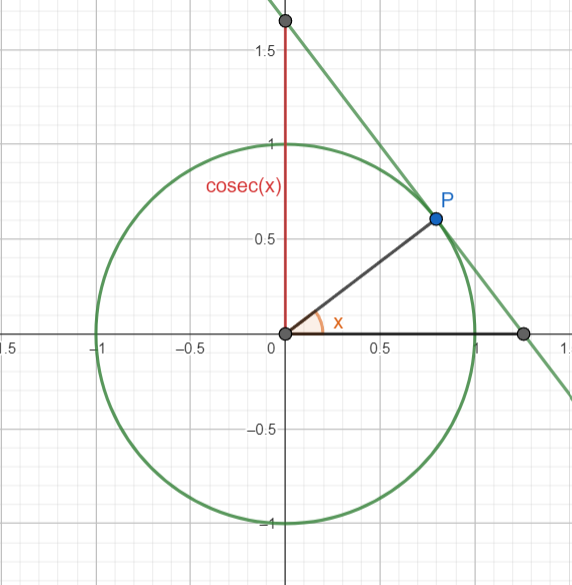
Funzione Cosecante Dato un triangolo rettangolo, la cosecante di uno dei due angoli acuti adiacenti all'ipotenusa è definito come il rapporto tra la lunghezza dell'ipotenusa e la lunghezza del cateto opposto all'angolo. Data la circonferenza goniometrica, la cosecante di un angolo è il reciproco del seno dell'angolo considerato.. Dopo un giro completo della circonferenza, la cosecante assume sempre gli stessi valori, per questo diremo che è periodica di periodo 2π (180°) La funzione cosecante è dispari, quindi simmetrica rispetto all'origine degli assi cartesiani.