www.sansonettiivano.it

SOMMA VETTORI

Introduzione alla Somma dei Vettori Il concetto di vettore trova la sua origine nell'ambito della Fisica in quanto in essa la descrizione basata solo su grandezze elementari quali per esempio il tempo, la massa, la temperatura, il volume, si dimostra ben presto inadeguata alla rappresentazione degli oggetti e delle loro relazioni. Le grandezze fisiche si distinguono essenzialmente in due grandi classi. Quelle che risultano completamente definite quando se ne conosce la sola misura rientrano nella categoria delle grandezze scalari le altre richiedono di norma un maggior contenuto informativo e vengono rappresentate dalle grandezze vettoriali. Due vettori si dicono: equipollenti quando hanno la stessa direzione, lo stesso verso e uguale modulo; concordi se hanno stessa direzione e stesso verso; discordi quando hanno stessa direzione e verso contrario; opposti se hanno uguale intensità e sono discordi. Metodi di Calcolo della Somma dei Vettori Per calcolare la somma tra due vettori possiamo utilizzare il metodo punta-coda oppure il metodo del parallelogramma (La somma di due vettori sarà comunque sempre un vettore). 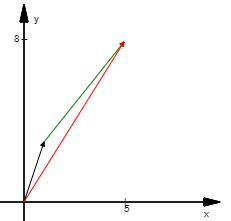Metodo punta-coda Tenendo fissato e un vettore (in questo caso \(\vec{a}\)), si trasporta l’altro (che qui per noi è \(\vec{b}\)), mantendolo sempre parallelo a se stesso, in modo tale che il suo punto di applicazione coincida con la punta del primo vettore. 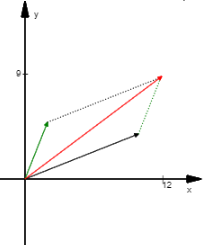Il vettore somma $$\vec{a}+\vec{b}=\vec{s}$$ è allora il vettore che congiunge la “coda del primo vettore”, ossia il suo punto di applicazione, con la “punta del secondo vettore”, come mostrato in figura:<\p> Metodo del parallelogramma Si uniscono le code dei due vettori, e si costruisce il parallelogramma che ha come lati i due vettori. La somma dei vettori corrisponde alla diagonale del parallelogramma:come mostrato in figura:<|p>

Simulatore Componente X Componente Y Vettore 1 (V1) Angolo descritto da "V1" in gradi Vettore 2 (V2) Angolo descritto da "V2" in gradi Somma (S) Angolo descritto da "S" in gradi

Scegli il metodo: Punta-Coda Parallelogramma